quantum teleportation

#quantum-computing

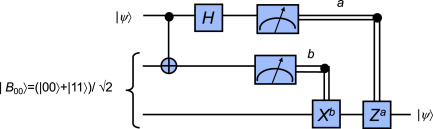
Suppose $| ψ ⟩ = α | 0 ⟩ + β 1 ⟩$ and they share the bell states $| ϕ^{*} ⟩ = \frac{1}{\sqrt{2}} (| 00 ⟩ + | 11 ⟩)$
The composite system becomes$$\frac{\alpha}{\sqrt2}(|0\rangle(|00\rangle + |11\rangle)) + \frac{\beta}{\sqrt2}(|1\rangle(|00\rangle + |11\rangle))$$

post CNOT$$\frac{\alpha}{\sqrt2}(|000\rangle + |011\rangle) + \frac{\beta}{\sqrt2}(|110\rangle + |101\rangle)$$
post Hadamard Gate$$\frac{\alpha}{\sqrt2}(|+\rangle |0\rangle |0\rangle + |+\rangle|1\rangle|1\rangle) + \frac{\beta}{\sqrt2}(|-\rangle|1\rangle|0\rangle + |-\rangle|0\rangle|1\rangle)$$
by rewriting we get$$\frac{1}{2}[|00\rangle(\alpha|0\rangle + \beta|1\rangle) + |01\rangle(\alpha|1\rangle + \beta|0\rangle) + |10\rangle (\alpha|0\rangle - \beta|1\rangle) + |11\rangle (\alpha|1\rangle-\beta|0\rangle)]$$
Now Alice measures the first two qubits:

Alice's Qubits post measurement	Transformations Bob has to make
00	I
01	X
10	Z
11	Y